教員紹介
秋田 美代 教授 (数学教育学)
ゼミ内容
「学習内容の理解を定着させる指導方法」「生徒の関心・意欲を高めるた めの 算数・数学的な活動をとりいれた教材開発」等、各自の教育課題に基 づいて研 究活動を行っています。そこでは、理論と実践の融合した指導方法の構築や教 材の作成等ができる ように、算数・数学の学習内容の構造についての分析や生 徒の学習過程に ついての分析も行っています。
過去の卒業研究の題目:
- 割合に対する児童の理解を深めるための研究ー数直線を用いた指導に焦点をあててー
- 分数のわり算を理解させるための指導についての研究
- 数学的な見方・考え方を働かせる学習の設計に関する研究–図形領域に焦点を当てて–
- 数学に対する自律的な問題解決能力の育成に関する研究–メタ認知に焦点を当てて–
- 既習事項を生かした算数の学びに関する研究
- 多様な見方・考え方を引き出す数学的活動に関する研究
研究内容
児童・生徒の認知過程における学習内容の構造的な理解に焦点を当て、基 礎的・ 基本的な内容を確実に定着し、算数・数学における創造性を高める 指導法を開 発することを目的とした研究を行っています。児童・生徒の算数・数学に対す る興味・関心を引き出し、算数・数学学習 に主体的に取り組む態度及び数学的 思考力・創造力を身に付けさせる指導 法を開発し、開発した指導方法を小学校 算数・中学校数学の学習指導に適 用し役立てることをねらいとしています。

宮口 智成 教授 (数理科学)
学部授業の主な内容
- 確率・統計学: 場合の数, 確率の基礎, 確率変数, 確率分布, 確率密度関数
- 確率・統計学特論 (各年開講): 大数の法則, 相関係数, 最小二乗法
- 計算数学: 初等数学の問題をプログラミングを活用して調べます. プ ログラミング言語には Excel VBA もしくは Python を用います.
- 計算数学特論 (各年開講): コンピュータを活用して統計学の基礎につ いて学びます。推定と検定についても解説します。
- 基礎情報教育I (4 人で分担): 8 コマ担当し、データ科学の基礎につ いて解説・実習を行います. ホームページは こちら。
- 人口と食糧問題 (3 人で分担): 5コマ担当し、人口に関する統計分析 について解説します。講義スライドは こちら からダウンロードできま す。
ゼミ内容 (卒業研究)
確率統計学あるいは数理科学関係の諸問題について、解析的手法と数値的手法 (コンピュータによる数値計算) を用いて調べていきます。学生の興味に合わせ てテキストを 1 冊選び、週 1 回のゼミを行います。
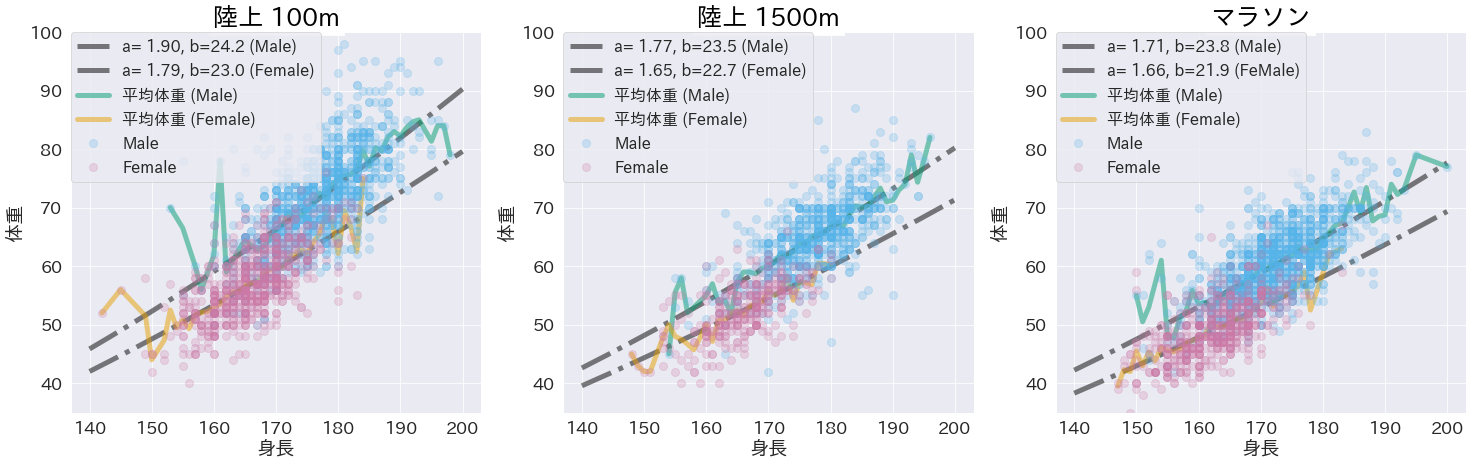
卒業研究の例 (オリンピック出場選手の体重・身長の散布図)。競技毎・男女毎 に最小二乗法を用いて、\(\text{(体重)}= b\text{(身長)}^a\) という関数を求 めています (黒い点鎖線)。 \(a=2\) のとき、 \(b\) は Body Mass Index (BMI) に対応しますが、上の例では \(a\) の値は 2 より若干小さいことが分かります。
過去の卒業研究の題目:
- ランダム生成した三角形における最大角の確率分布
- 秘書問題において上位層を採用する戦略と確率
- 統計と確率をつなぐ授業開発〜乱数ゲームにおける一致数の分布〜
- パロンドーの確率ゲームの解析〜パラドックスが生じる条件〜
- 路上駐車の数理モデル〜車両間スペースの解析〜
- マルコフ連鎖を用いた野球の打順解析
- 教員採用者数の予測: マルコフ連鎖を用いた解析
研究内容
物理や生物などに見られる現象と関わる数理モデルを、理論計算とコンピュー タを用いて調べています。数理モデルとして、確率過程や非線形力学系などを 用います。特に最近はコロイド分散系の数理モデル (下の式) の生物学への応 用について研究を進めています。
\begin{equation} \frac {\partial }{\partial t} P(\vec{R}, t) = \sum_{i,j=1}^{N} \nabla_i \cdot \vec{D}_{ij} \cdot \left\{ \beta \Bigl[\nabla_j\Phi(\vec{R}) \Bigr] P(\vec{R}, t) + \nabla_j P(\vec{R}, t) \right\} \end{equation}

早田 透 准教授 (数学教育学)
学部授業の主な内容
- 数学科教材論: 学校教員として知らなければならない数学の知り方とは 何か。学習を設計するとは,カリキュラムを編成するとは,どういうこと か。そして,教材研究とはどの様に実施するものかを,具体的な演習を通 して学んでいきます。
ゼミ内容
過去の卒業研究の題目:
- 算数教科書における 0 の記述に関する研究-−EIS 原理を視点として−-
- 中学校数学における証明の構想と構成に関する研究–分野による違いに着目して–
- プラクセオロジーを用いた算数教科書の記述研究〜図形領域に着目して〜
- 割合の単元における教科書の条件と制約に関する研究

山中 仁 准教授 (幾何学)
学部授業の主な内容
- 幾何学Ⅰ:
- 幾何学Ⅱ:
- 幾何学Ⅲ:
- 幾何学特論:
ゼミ内容
過去の卒業研究の題目:
- 幾何と解析から見た2次漸化式
- 結び目とコンウェイ多項式
- 格子多角形とエルハルト多項式

宇田川 陽一 講師 (解析学)
主な学部授業
- 解析学Ⅰ:
- 解析学Ⅱ:
- 解析学Ⅲ:
- 解析学特論:
ゼミ内容
研究内容
